
In order to solve the problems on Venn diagrams with three sets, the formula is as follows: Given below is a Venn Diagram for three sets: When all three circles overlap, the overlapping parts show the elements that are either common to any two circles or they are common to all three circles. Venn Diagram for three sets is also called a 3-circle Venn diagram. Venn Diagrams for three sets are made up of three overlapping circles in which the three circles show how the elements of the three sets are related. It represents elements of set A which are not there in set B. The region covered by set A, excluding the region that is common to set B, is the difference between sets A and B. Sometimes, it is referred to as a relative complement. This represents elements of the universal set that are not common between sets A and B. (A ∩ B)’ is read as the complement of set A intersecting set B. This represents elements that are neither in set A nor in set B. (A ∪ B)’ is read as the complement of A union B. The properties of the complement of the set are as follows: The region covered in the universal set, excluding the region covered by set A, will give the complement of A. This set has all the elements that are absent in set A. The properties of the intersection of sets are as follows:Ī' is the complement of set A. The region that is common to both circles denotes the intersection of Set A and Set B. The intersection of sets is represented using a Venn diagram with two intersecting circles. The union of two sets A and B is given by A ∪ B =. The representation of the following operations on sets using Venn Diagrams are as follows: In the set theory, there are various operations performed on sets which are described as follows: The first circle represents the Indoor Animals, the second circle denotes the Outdoor animals and the common part shows both Outdoor and Indoor animals. Here, the rectangle shows the universal set, i.e. Both Outdoor and Indoor: Rabbits and Fish.Outdoor Animals: Horses, Tortoises, and Goats.Indoor Animals: Cats, Hamsters, and, Parrots.Step 4: Lastly, put all the elements in the relevant circles.Įxample: Given below is a Venn diagram for the Indoor and Outdoor Animals.Step 3: Next step is to draw the circles according to the categories.Step 2: Now, draw a rectangle and mark it as per the correlation between the sets.Step 1: First, categorize all the elements into sets.
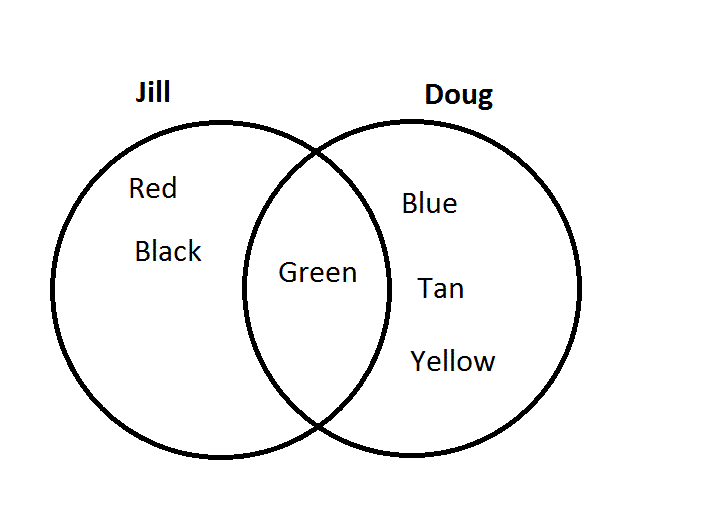
Here are the steps to draw a Venn Diagram: Also, they are part of a bigger rectangle, making them the elements of the universal set. All the elements of the set should be inside the circle. Every set is a subset of the universal set, meaning that every other set will be inside the rectangle that represents the universal set. In order to draw a Venn diagram, first the universal set should be known. It means the elements that do not belong to set A. It means the elements that belong to both sets A and B.Ī' is read like ‘A complement’.
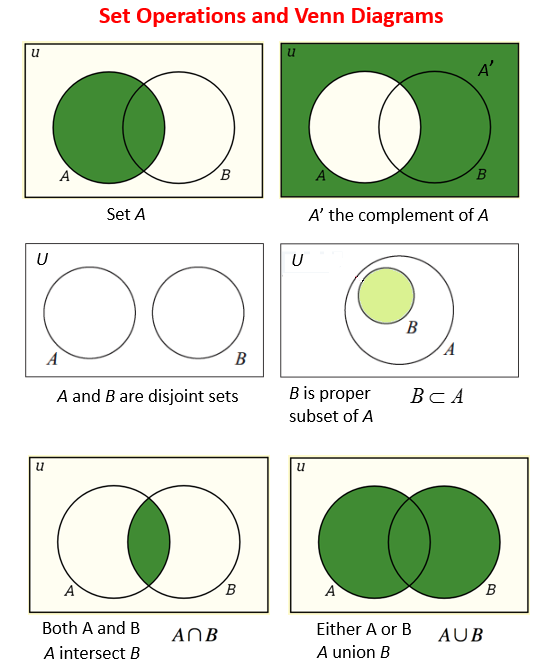
It means the elements that belong to either set A or set B or both sets.Ī ∩ B is read like ‘A intersection B’. Here, circle A is contained within circle B which means all the elements of A are elements of set B.Ī ∪ B is read like ‘A union B’. For instance, in the given Venn diagram of two sets A and B, A is a subset of B.


 0 kommentar(er)
0 kommentar(er)
